Dictionary¶
Here are explained some usefull terms.
PD code and EM code¶
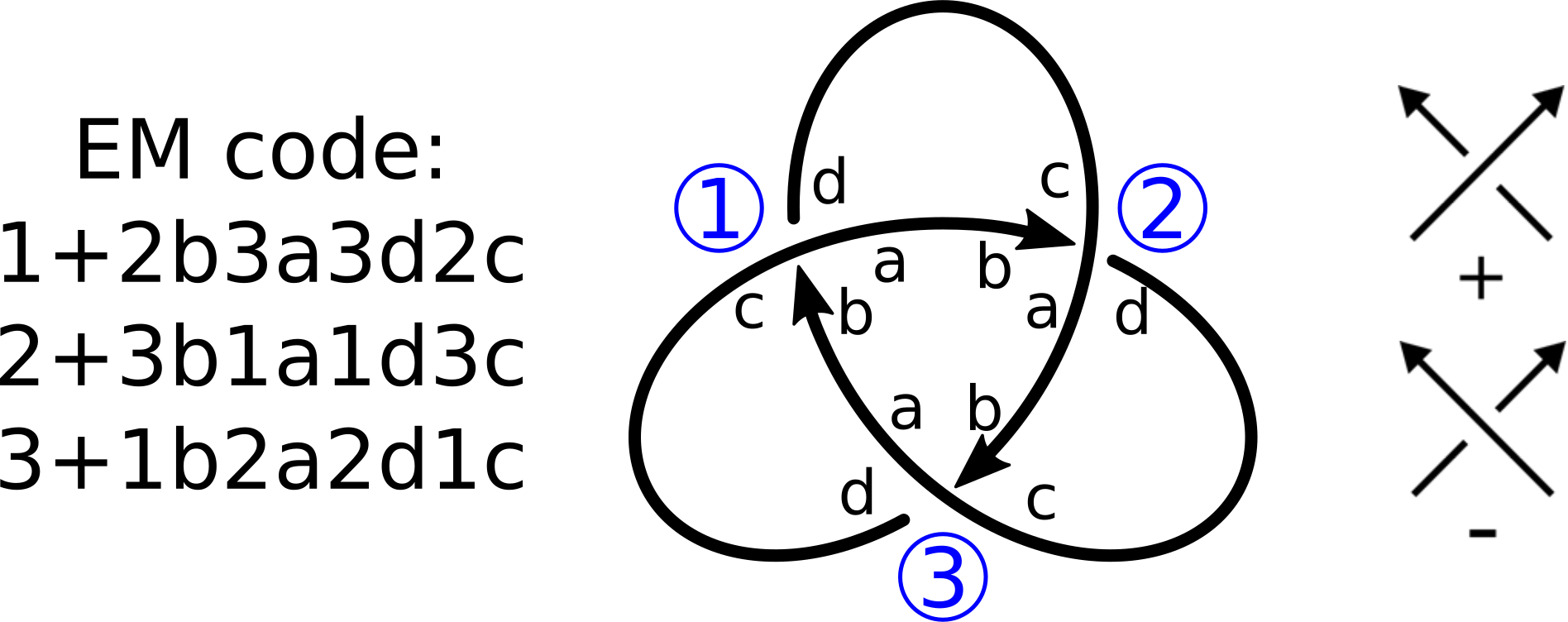
EM code (Ewing-Millett code) and PD code (planar diagram code) are methods of descirbing knots in detail. To find EM code of your knot diagram:
Give each crossing a number,
Give each crossing a sign according to,
For each crossing:
Name “a” direction of outgoing overpassing arc,
Name every other direction in a clockwise order “b”, “c” and “d”,
In this way, every arc – by which we mean here continuous piece of chain between two neighbour crossings – consists of two ends, each described by a number and a letter.
A code for a crossing consists of its number, its sign, and four two-character descriptions of opposite ends of four arcs coming out of the crossing (in order “a”, “b”, “c”, “d”).
A code for a structure consists of a list of codes for crossings.
Finding PD code is easier:
Go along the structure according to its orientation and after each crossing asign next number to it (starting from 1).
Each crossing is described by “X” symbol with numbers of its neighbouring arcs: counter-clockwise starting from ingoing underpassing.
Structure code is described by a list of its crossings.
In case of spatial graphs (theta-curves, handcuffs) PD code can be extended. In such a case every vertex connected to three arcs is described by “V” symbol with numbers of its neighbouring arcs in any order.

Reidemeister moves¶
Set of basic moves that change knot diagram but doesn’t alter knot topology.
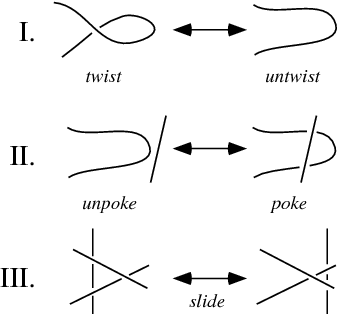
Three types of Reidemeister moves¶
KMT algorithm¶
Based on Koniaris’s and Muthukamar’s method. This algorithm analyzes all triangles in a chain made by three consecutive points, and removes the middle point in case a given triangle is not intersected by any other segment of the chain. In effect, after a number of iterations, the initial chain is replaced by (much) shorter and simpler chain of the same topological type.
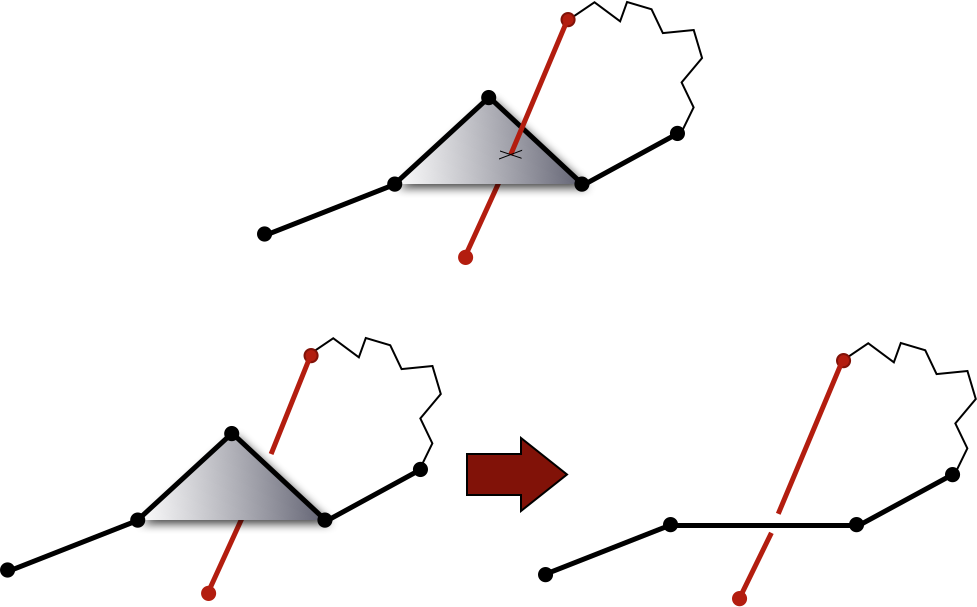
Representation of KMT algorithm¶